动手学深度学习
阅读《动手学深度学习》时的笔记
预备知识
tensor.shape 沿每个轴的长度
tensor.numel() 元素个数
tensor.reshape(a,b) 用-1来自动计算剩下的维度
@是矩阵乘法,*是矩阵元素相乘
广播机制:行向量与列向量相加时行向量复制行,列向量复制列。
X[:] = X + Y和X += Y不会分配新内存
X.numpy() 将tensor转ndarray
torch.tensor(X) 将ndarray转tensor
a.item() 大小为1的张量转标量
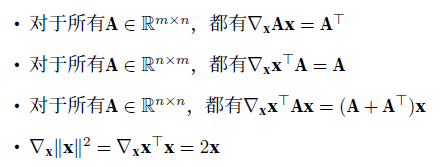
范数
用于表征向量的大小。
\(L_2\)范数\(||\vec x||_2=\sqrt{\sum_{i=1}^nx_i^2}\)
\(L_1\)范数\(||\vec x||_1=\sum_{i=1}^n|x_i|\)
\(L_p\)范数\(||\vec x||_p=(\sum_{i=1}^n|x_i|^p)^{1/p}\)
线性神经网络
线性回归
解析解 \[ \vec w = (X^TX)^{-1}X^T\vec y \]
小批量随机梯度下降(minibatch stochastic gradient descent)
随机抽样一固定样本数量的小批量\(\Beta\) \[ (\vec w,b)\leftarrow(\vec w,b)-\frac{\eta}{|\Beta|}\sum_{i\in\Beta}\partial_{(\vec w,b)}l^{(i)}(\vec w,b) \] 也即 \[ \vec w\leftarrow\vec w-\frac{\eta}{|\Beta|}\sum_{i\in\Beta}\partial_{\vec w}l^{(i)}\vec w\\ b\leftarrow b-\frac{\eta}{|\Beta|}\sum_{i\in\Beta}\partial_{b}l^{(i)}b \]
softmax回归
解决分类问题,one-hot编码
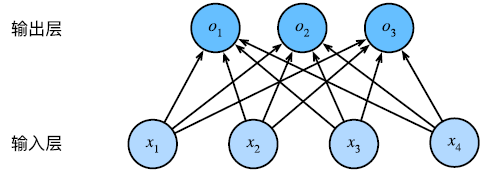 \[
\vec o=\matrix W\vec x + \vec b
\]
\[
\vec o=\matrix W\vec x + \vec b
\]
为了使输出的概率维持在0~1之间,需要对输出做校准(calibration),即通过softmax函数。 \[ \hat {\vec y} = softmax(\vec o),其中\hat {y_j} = \frac {exp(o_j)}{\sum_k exp(o_k)} \] 损失函数为 \[ \begin{align} l(\vec y, \hat{\vec y}) =& -\sum_{j=1}^qy_jln\hat {y_j},q为独热编码向量的长度\\ =& ln\sum_{k=1}^q exp(o_k)-\sum_{j=1}^qy_jo_j \end{align} \] 导数为 \[ \part_{o_j}l(\vec y, \hat {\vec y})=\frac{exp(o_j)}{\sum_{k=1}^qexp(o_k)}-y_j=softmax(\vec o)_j - y_j \]
为加速计算,往往对小批量数据采用矢量化的操作。如果用\(\matrix X\)表示批量的样本,一行为一个样本的所有特征,则 \[ \begin{align} \matrix O=&\matrix X \matrix W + \vec b\\ \hat {\matrix Y}=&softmax(\matrix O) \end{align} \] 其中,\(\hat {\matrix Y}\)的一行对应一个样本的预测结果。
实际使用中,由于\(exp(o_j)\)容易发生上溢,往往要进行规范化的操作。 \[ \begin{align} \hat{y_j} =& \frac{exp(o_j-max(o_k))exp(max(o_k))}{\sum_k exp(o_k-max(o_k))exp(max(o_k))}\\ =&\frac{exp(o_j-max(o_k))}{\sum_kexp(o_k-max(o_k))} \end{align} \] 如果用该计算结果计算交叉熵,由于精度限制,会出现下溢。所以计算交叉熵不能直接使用该计算结果,而应使用下式。 \[ \begin{align} log(\hat{y_j})=&log(\frac{exp(o_j-max(o_k))}{\sum_kexp(o_k-max(o_k))})\\ =&o_j-max(o_k)-log(\sum_k exp(o_k - max(o_k))) \end{align} \]
多层感知机(Multilayer Perceptron, MLP)
多层感知机是最简单的深度网络。
直接地在线性神经网络中添加层并不能使我们的模型表达更复杂的结构,它依然会退化为线性模型。所以,在仿射变换之后,还需要对每个隐藏单元应用非线性的激活函数\(\sigma\)。激活函数的输出被称为活性值(activations)。 \[ \begin{align} \matrix H=&\sigma(\matrix X \matrix W^{(1)} + \vec b^{(1)})\\ \matrix O=&\matrix H\matrix W^{(2)}+\vec b^{(2)} \end{align} \]
通常,为了更高效的内存在硬件中的分配和寻址,层的宽度选择2的若干次幂。
常见的激活函数
修正线性单元(Rectified linear unit,ReLU) \[ ReLU(x)=max(x, 0) \] 它有一些变体如参数化ReLU(pReLU),\(pReLU(x)=max(0,x)+\alpha min(0, x)\)
sigmoid函数(也叫挤压函数) \[
sigmoid(x)=\frac{1}{1+exp(-x)}
\] 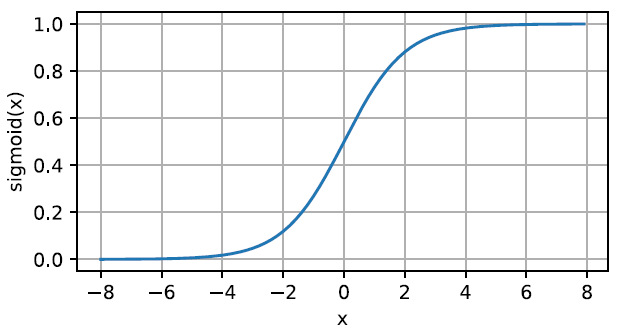
导数为\(sigmoid(x)(1-sigmoid(x))\)
tanh函数(双曲正切) \[
tanh(x)=\frac{1-exp(-2x)}{1+exp(-2x)}
\] 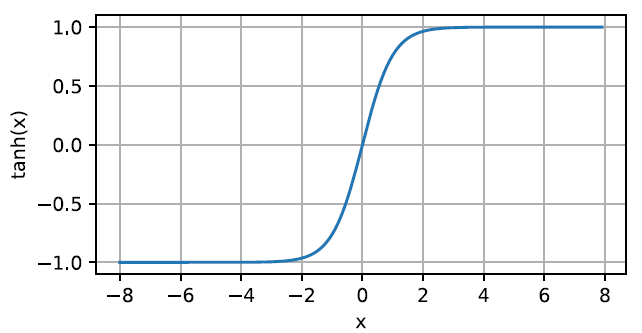
导数为\(1-tanh^2(x)\)
模型选择、欠拟合和过拟合
用于对抗过拟合的技术称为正则化(regularization)
容易引起过拟合的原因:
- 可调整参数数量过多
- 参数的取值范围较大
- 训练样本数量较少
数据集处理
K折交叉验证
当训练数据稀缺时,将原始训练数据分成K个不重叠的子集,然后执行K次模型训练和验证,每次在K-1个子集上进行训练,并在剩余一个子集上进行验证,最后通过对K次实验的结果取平均来估计训练和验证误差。
正则化技术
范数与权重衰减
权重衰减(weight decay)是最广泛使用的正则化技术之一,通常也被称为\(L_2\)正则化,这项技术通过函数与零的距离来衡量函数的复杂度。
为保证权重向量比较小,常用方法是将范数作为惩罚项加入到损失函数中。
\(L_1\)正则化线性回归通常被称为套索回归(lasso regression),会导致模型将权重集中在一小部分特征上,而将其他权重清除为零,称为特征选择。
\(L_2\)正则化线性模型构成经典的岭回归(ridge regression)算法,它对权重向量的大分量施加了巨大的惩罚,使得模型偏向在大量特征上均匀分布权重的模型。
对于一个样本,有 \[ L_2=L(\vec w, b)+\frac{\lambda}{2}||w||^2 \] \(L_2\)正则化回归的小批量随机梯度下降更新如下 \[ \vec w\leftarrow(1-\eta\lambda)\vec w-\frac{\eta}{|\Beta|}\sum_{i\in\Beta}\vec x^{(i)}(\vec w^T\vec x^{(i)}+b-y^{(i)}) \]
暂退法
向每一层添加无偏的噪声。
每个中间活性值h以暂退概率p由随机变量h'替换,即 \[ h'=\begin{cases} 0&,概率为p\\ \frac{h}{1-p}&,其他情况 \end{cases} \] 通常在测试时不会使用暂退法。